You can write me in case you are interested in accessing the source code. However, for obvious reasons, I cannot provide source code to ETH students enroled in CG course.
Features
- Images as texture
- Bump Mapping
- Textured Subsurface Scattering: Photon Beam Diffusion with Single Scattering
- Plastic and Rough-Plastic reflectance BSDFs
- Can be run with --nogui option
The --nogui option is useful to use the renderer in some enviorement that only has command line available, such a linux rendering cluster. Below is an screenshot of how the time remaining is also displayed when running in this mode.
Required Libraries
- Mitsuba core headers are included in "include/mitsuba" to be able to use Mitsuba implementation of an octree. Mitsuba headers need some dependences that must be installed in the system.
- CImg library is included in the ext folder and is used to read images for textures. CImg uses libpng to read transparency channels in png images so that library is required as well.
Images as textures
Features:
- Support for (png, tga and jpg) sRGB textures as well as textures with only one channel.
- Support for textures with transparency/opacity or alpha channel.
- Support for operations betwen textures with OpenMP: multiplication, sum, difference, division, exp(), and sqrt()
- Support for scaling and offsets (see scenes/normal-maps/stones/normal-stones-delta.xml and scenes/normal-maps/stones/normal-stones-modif.xml which use this functionallities).
Test scenes:


- Test Scene: scenes/textured_teapot/pattern_teapot.xml
- Mitsuba Reference Scene: scenes/textured_teapot/pattern_teapot_mitsuba.xml

Texture Map Implementation Files
- include/texture_bitmap.h
- src/texture_bitmap.cpp
- Use texture maps for diffuse BSDF albedo at src/diffuse.cpp
- The opacity for meshes its implemented at src/mesh.cpp:Mesh::rayIntersect
Bump Mapping (Normal Maps)

Test Scene at scenes/normal-maps/stones/normal-stones.xml
Normal Map Implementation Files
SubSurface Scattering (SSS) (and Rough-Plastic Reflectance)
Before begining to explain the implementation note that the untextured versions of SSS have slightly better performance and are available at the folder /src/subsurface/untextured and /include/subsurface/untextured. They are also easier to understand and thus is recommended to read that code before trying to understand the textured version. Regardless, the textured versions can still be used with single colors (the textured versions are always used for the following test scenes).Features
- Support for precomputed irradiance map that takes into account direct and indirect illumination.
- Plastic and Rough-Plastic reflectance BSDFs
- Bitmaps for Rough-Plastic roughness (aka glosiness) and specularity
- Support for Dipole, Better Dipole, and Photon Beam Diffusion (PBD) profiles.
- Reparametrization of Dipole and Better Dipole (and PBD) with diffuse reflectance and diffuse mean free path.
- Support of textures maps for the three SSS models
Irradiance Map
My implementation follow a two-pass algorithm explained in "A Rapid Hierarchical Rendering Technique for Translucent Materials" [p576-jensen] that permits to render translucent materials in a fast way.
- Precomputation of arriving irradiance at different sampled points on the suface of the object.
- Evaluation of BSSRDF aproximations using the precomputed irradiance samples stored in a octree.
- To evaluate the exitant radiance at a point the diffusion model is applied to all the stored irradiance samples. However, computing the model for all the samples its very costly and instead the it is computed hierarchically traversing an octree that contains the samples.
The precomputation step is done with OpenMP: points are sampled uniformly in the surface using an independent sampler and then the irradiance computed at that point calling to Integrator::E() method. To reduce the number of sampling points required to not have splotches artifacts a better sampling strategy could be used, point repulsion is mentioned in PBD reference paper [habel13pbd]. Mitsuba core has been used for the octree. irrtree.cpp contains the code for the tree transversal which is also almost identical to Mitsuba implementation with the only difference that the length of the beams is also taken into account: this is needed for PBD implementation which does an aditional precomputation step to store the length of the normally incedent beams at the sampled points.
The following scene contains a teapot and a cylinder with SSS materials using a direct-illumination irradiance map. Mitsuba dipole implementation has been used as a reference. The material properties used correspond to "Chocolate Milk (regular)" in "Acquiring Scattering Properties of Participating Media by Dilution" [Acquiring].




- My Dipole: scenes/subsurface/teapot/plasticteapot_direct_mis.xml
- My Better Dipole: scenes/subsurface/teapot/plasticteapot_better_direct_mis.xml
- My Photon Beam Diffusion + Single Scattering: scenes/subsurface/teapot/plasticteapot_pbd_direct_mis.xml
- Mitsuba Dipole: scenes/subsurface/teapot/plasticteapot_direct-mitsuba.xml
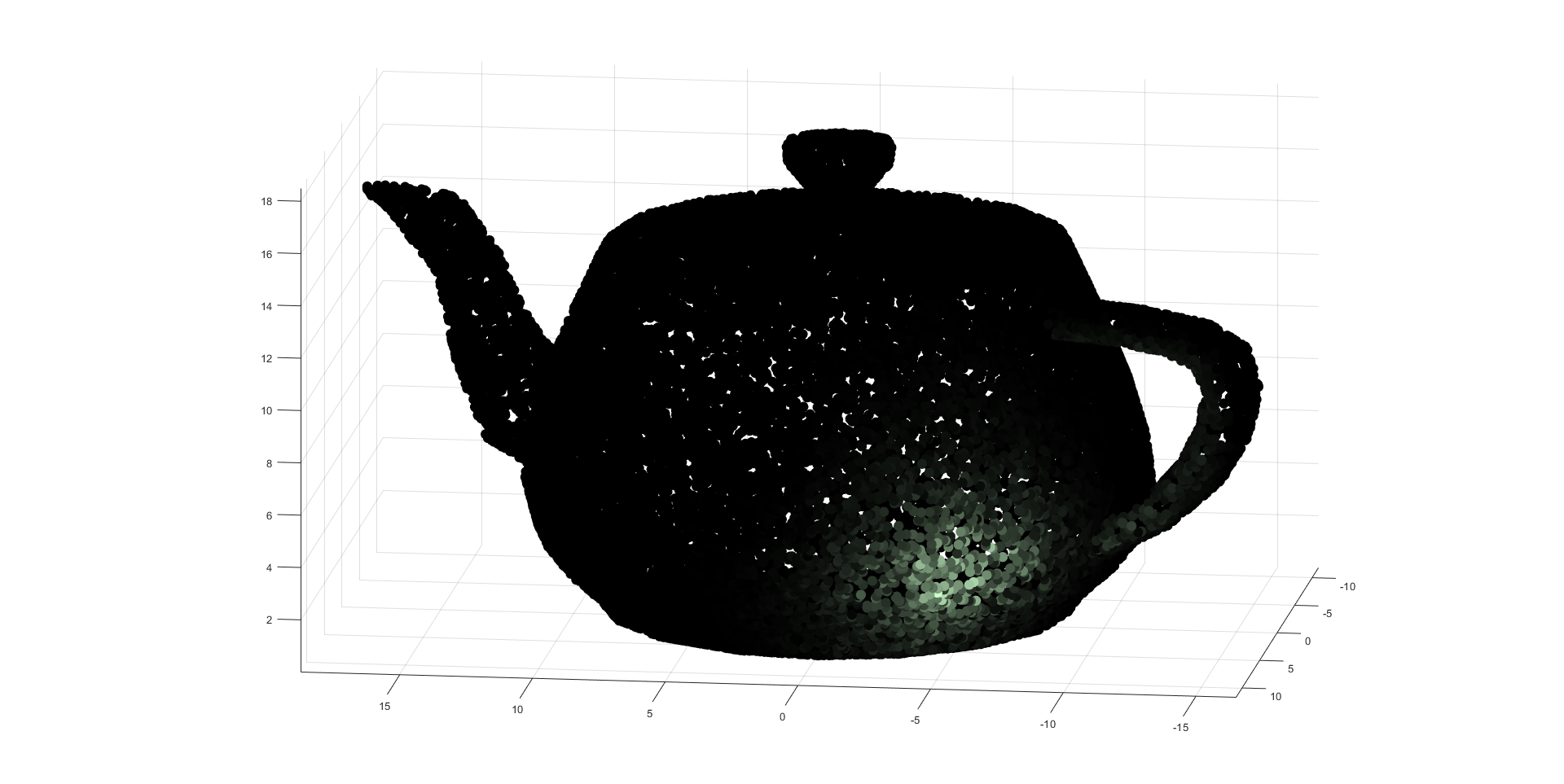
For debugging and validation purposes the implementation can export the irradiance samples (implementation at and ) a ".ply" file format that stores a colored point cloud. The files can be visualized with matlab (scenes/subsurface/teapot/plasticteapot_direct_mis.m). Below is the irradiance map for the previous scenes. The exporter needs to be activated with "#define EXPORT_IRRADIANCE" in "src/subsurface/pointbasedsubsurface.cpp".
The implementation can use compute the irradiance arriving from indirect illumination using the same integrator the scene is being rendered with (for direct integrator, only one bounce). This feature is turned off by default but can be turned on setting "irrIndirect" property to true (see xml for scene below). The following scene (.xml) has been used for testing purposes: it contains a teapot and a cylinder to which illumination only arrives indirectly and thus if global illumination is disabled we wouln't be able to see those objects.




- My Dipole: scenes/subsurface/teapot/teapot_GI_path_mis.xml
- My Better Dipole: scenes/subsurface/teapot/teapot_GI_betterd_path_mis.xml
- My Photon Beam Diffusion: scenes/subsurface/teapot/teapot_GI_PBD_path_mis.xml
- My Photon Beam Diffusion + Single Scattering: scenes/subsurface/teapot/plasticteapot_GI_PBD_SC_path_mis.xml
- Mitsuba Dipole: scenes/subsurface/teapot/plasticteapot_GI_path-mitsuba.xml
As can be appreciated the PBD still has some numerical incosistencies in the implementation which cause some black splotches. For some materials and for some lighting conditions the current implementation can be unstable. However as can be seen in the materials examples section, I still have been able to render some PBD materials without any problems.
To be physically accurate, the SSS objects must use a BSDF that only accounts for specular reflection since the SSS is already responsible for all internal scattering. For this reason, I have implemented the specular reflectance component of a dielectric and rough-dielectric material.




- plastic specular reflectance: scenes/subsurface/teapot/fullplasticteapot_GI_path_mis.xml
- rough plastic specular reflectance: scenes/subsurface/teapot/fullroughplasticteapot_GI_path_mis.xml
- mitsuba plastic specular reflectance: scenes/subsurface/teapot/fullplasticteapot_GI_path-mitsuba.xml
- mitsuba rough plastic specular reflectance: scenes/subsurface/teapot/fullroughplasticteapot_GI_path-mitsuba.xml
Irradiance Map Implementation Files
- Precomputation Step and evaluation of BSSRD
- Precomputation step: src/subsurface/pointbasedsubsurface.cpp - PointBasedSubsurface::preprocess()
- Aditional Precomputation Step needed for PBD: src/subsurface/photonbeamdiffusion.cpp - PhotonBeamSubsurface::preprocess_samples()
- Evaluation of exitant radiance: src/subsurface/pointbasedsubsurface.cpp - PointBasedSubsurface::Lo()
- include/subsurface>pointbasedsubsurface.h
- Irradiance evaluation at a point in the surface
- Irrandiance Samples Exporter
Diffusion Aproximation Profiles
The Classic Dipole Aproximation can be easily improved adjusting boundary conditions ("Better Dipole" or "Improved Diffusion Model") as explained in "A Better Dipole" [betterdipole]. The Photon Beam Diffusion [habel13pbd] implementation is based on the better dipole aproximation but using Monte Carlo Integration to evaluate the better dipole profile at different depths in a beam. The implemented PBD model only considers normally incident beams.
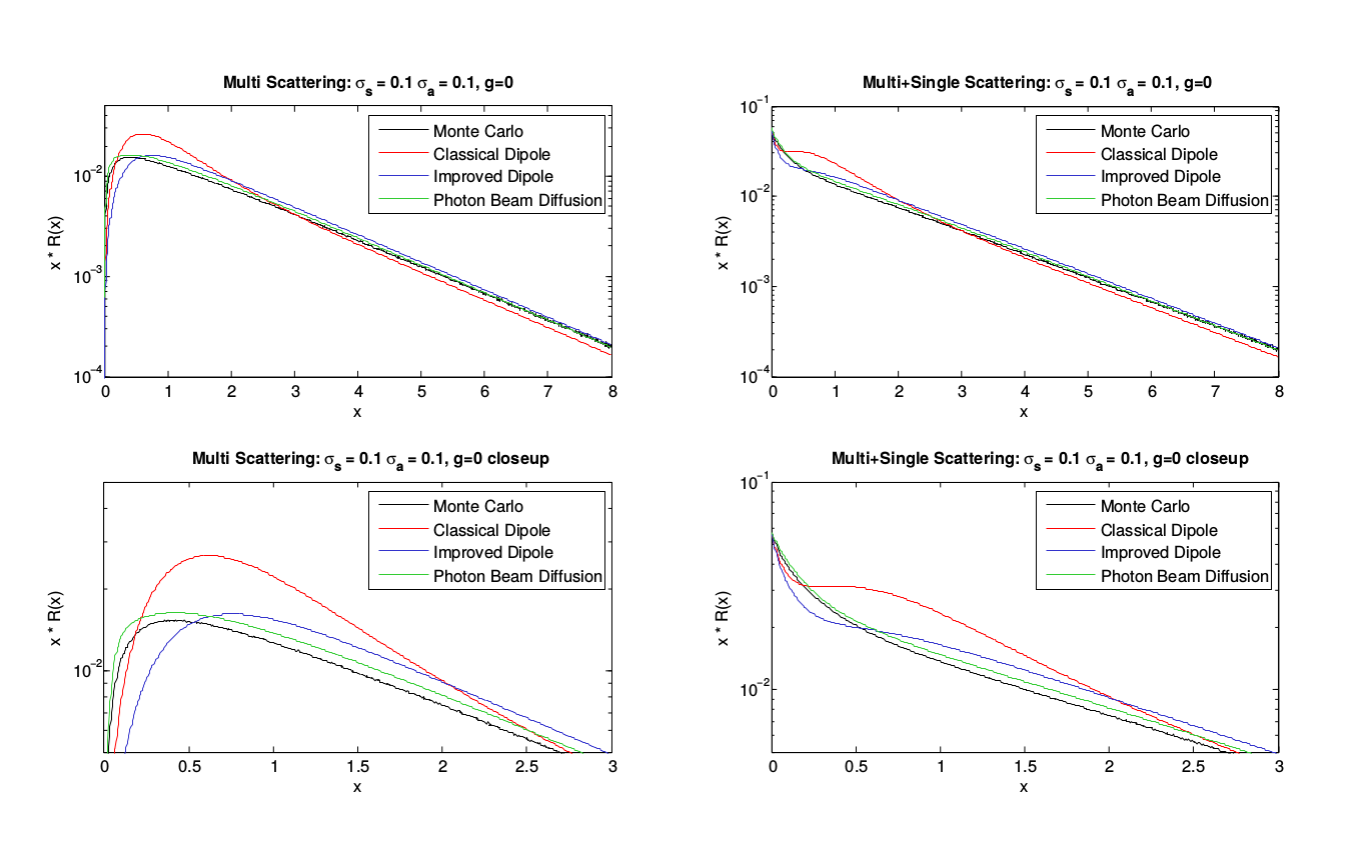
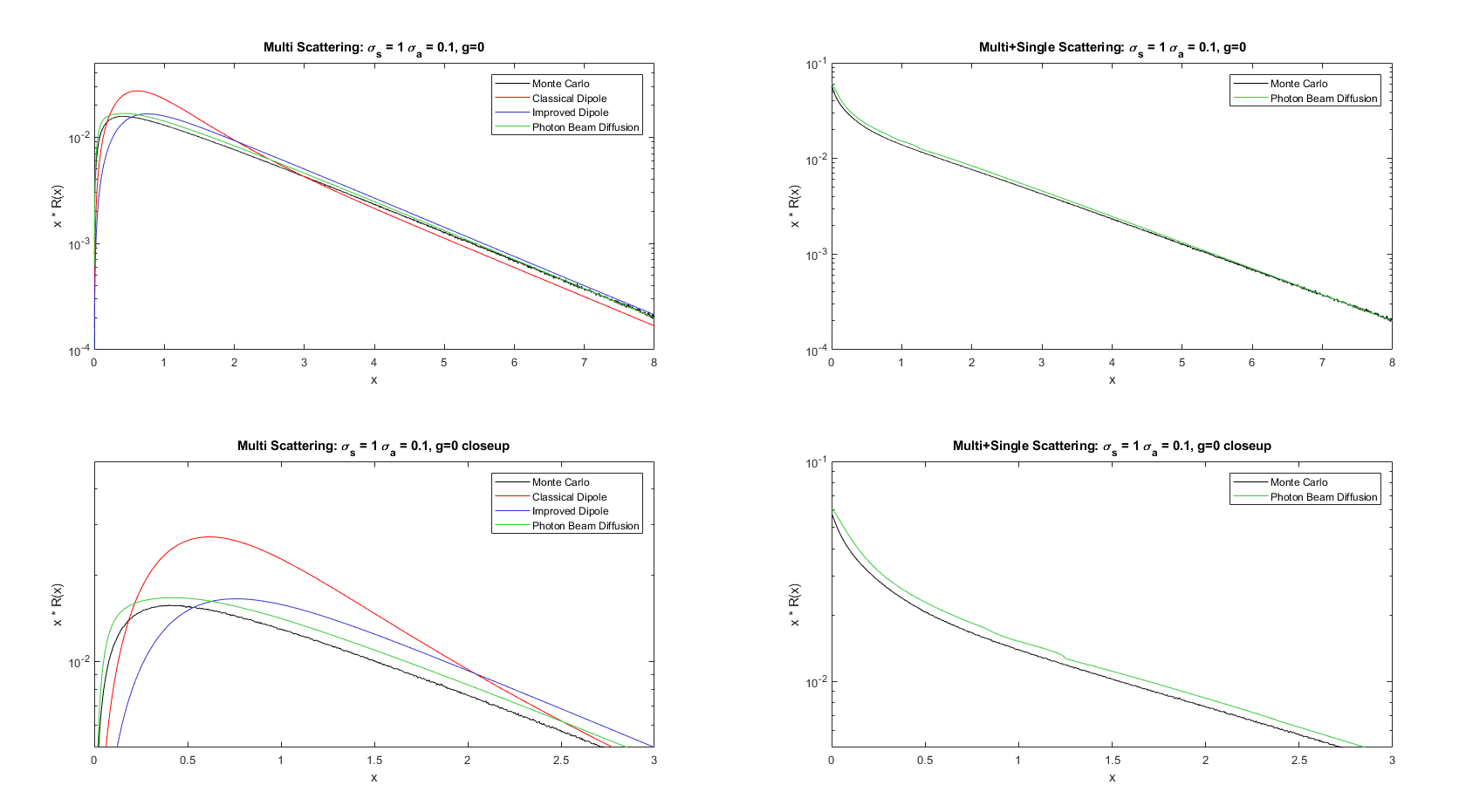
All diffusion profiles implemented have been tested for correctness against a matlab reference implementation from the PBD paper [habel13pbd] available at Pixar website. The profiles can be generated by evaluating the diffusion profile at different distances on the surface. The profiles are exported into an ascii txt file and plotted with matlab, the matlab reference implementation comes with a profile of a reference Monte Carlo solution and Single Scattering term, so we can plot those as well.
Profile results of my implementation and the profiles of the reference implementation (note there is a mistake in the plot, Sigma-s is 1 and not 0.1 since in their code they use 1 to compute the profiles).
Diffusion Aproximation Profiles
- Dipole Diffusion Profile and SSS: src/subsurface/dipole.cpp
- Better Dipole Diffusion Profile and SSS: src/subsurface/photonbeamdiffusion.cpp
- Dipole Diffusion Profile and SSS: src/subsurface/photonbeamdiffusion.cpp
- Profiles Generator: src/subsurface/untextured/profiles.cpp
- Dipole: scenes/subsurface/profiles/ClassicalDipole_0.1.txt
- Better Dipole: scenes/subsurface/profiles/ImprovedDipole_0.1.txt
- PBD: scenes/subsurface/profiles/PBD_0.1.txt
- PBD with Single Scattering: scenes/subsurface/profiles/PBD_SC_0.1.txt
- Plotting of profiles: scenes/subsurface/profiles/plotBSSRDFs.m
- ascii profiles:
Reparametrization
It is difficult to predict the appareance of the material by only tweaking the scattering and absorption coefficients. Instead, it is possible to achieve the same SSS results for a material in the dipole implementation using the diffuse reflectance and diffuse mean free path parameters as is described in sec. 4 in [p576-jensen]. For the better dipole (and PBD, which is based on the better dipole - although this reparametrization des not take into account the Single Scattering term) this reparametrization is slightly more complex but can also be achieved as is explained in [tbd] (the paper contains a reference implementation).
For example, given the scattering properties of marble [bssrdf, fig. 5] and using the reparametrization we can know that we can obtain the same results using the diffuse reflectance (0.856397, 0.821733, 0.7872219) and diffuse mean free path (85.094116, 55.661804, 39.512661). For the better dipole this values are (1.764425, 1.677361, 1.593446) for the diffuse and (85.134865, 55.705273, 39.559277) for the mean free path. The following scenes showcase how it is possible to achieve the same results using these more friendly parameters, in each case we render using the scattering parameters and then we do another identical render using the friendly parameters.


- Dipole Scattering Parameters: scenes/subsurface/marble_blocks/white_big_block.xml
- Dipole Parametrized: scenes/subsurface/marble_blocks/parametrized_white_big_block.xml




- Better Dipole Scattering Parameters: scenes/subsurface/marble_blocks/better_white_big_block.xml
- Better Dipole Parametrized: scenes/subsurface/marble_blocks/parametrized_better_white_big_block.xml
- PBD+SC Scattering Parameters: scenes/subsurface/marble_blocks/pbd_white_big_block.xml
- PBD+SC Parametrized: scenes/subsurface/marble_blocks/parametrized_pbd_white_big_block.xml
The following scenes also show how it is possible to embed the materials properties in textures. Note how the white marble in the texture matches the desired white marble (using the same method).




- Dipole Textured: scenes/subsurface/marble_blocks/textured_block.xml
- Better Dipole Textured: scenes/subsurface/marble_blocks/better_textured_block.xml
Reparametrization Implementation Files
- include/subsurface/subsurface.h
- src/subsurface/subsurface.cpp
- Reparametrization for dipole: src/subsurface/dipole.cpp - Rd() and rdToAlphap()
- Reparametrization for better dipole: src/subsurface/betterdipole.cpp - Rd() and rdToAlphap()
SSS Material Examples
The reparametriztion now allows us to use textures which contain the desired diffuse color. Realistic materials can be achieved by multiplying texture by the matching diffuse reflectance and diffuse mean free path of a real measured material. For all marble materials I use real marble properties described in [bssrdf, fig. 5] and for grapes and apple I also use the apple properties in the same paper.
The scenes for the following materials are available at scenes/subsurface/materials
Raw Marble:




Red Marble with golden splotches:




Red Marble:




Exotic Zebra Marble:




Apple:


Apple (untextured):




Grapes:


Final Sample Scene
